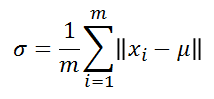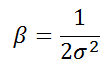저번에 참고한 URL을 기반으로 RBFN을 설명하자.
자세히 들어가기 전에, 우선 MLP를 학습할 것을 권장하며, 설명도중 언급되지는 않겠지만 '학습과정'과 '학습 후 분류과정'을 함께 설명하고 있기 때문에, 이해도중 헷갈릴 경우 과연 어떤 과정중을 설명하는지를 잘 생각해 보자.
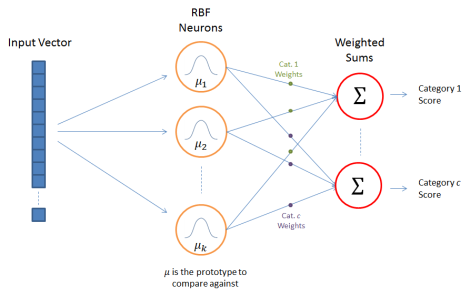

RBFN은 training set에 대한 input의 유사도를 측정한다. 각 RBF Neuron은 prototype를 저장하고있다.
새로운 입력이 들어오면 입력값과 prototype간의 유클리디안 거리를 계산한다.
위 RBFN의 구성은 아래와 같다.
1.input vector
2.RBF Neurons
3.output nodes
1. input vector
우리가 분류하길 원하는 n차 벡터를 의미한다. 모든 입력벡터들이 RBF뉴런에 반영된다.
(그림상 왼쪽의 푸른 n차 사각형을 의미)
2. RBF Neurons
각 RBF neuron마다 별개의 prototype벡터를 가지고 있다. 각 RBF neuron은 입력된 벡터와 해당 뉴런의 prototype간의 유사도를 비교한다. 따라서 출력은 0에서 1 사이의 값으로 이 값이 유사도를 의미한다. 입력값이 prototype과 같을경우 출력은 1이고 유클리디안 거리로 계산한 유사도가 멀 경우 출력은 0에 가까워 진다. RBF neuron의 출력은 bell curve(정규분포)를 따른다.
뉴런의 응답값은 활성화값이라 불린다.
또한 prototype벡터는 해당 뉴런의 center(중앙값)이라 불리운다. 즉, 이 center value는 bell curve의 중앙값임을 나타낸다.
3. Output Nodes
위의 category(범주)라는 단어 때문에 헷갈릴 수 있지만, 출력(output)은 우리가 원하는 총 m개의 출력범주로 이루어져 있다.
i개의 input을 넣고 m개의 서로 다른, 우리가 판단해야할 출력으로 이루어져 있는 것이다.
output node의 값은 연관된 카테고리(출력값)에 대한 score(점수)를 계산한다. 패턴인식에서 보자면 가장 높은 score를 가진 출력값이 '정답, 참값'등이 된다.
MLP를 했다면 당연히 알겠지만 해당 카테고리는 뉴런의 갯수(k)만큼의 활성화 값과 가중치의 곱으로 계산되어지며 각 카테고리마다 뉴런 대 output node를 이어주는 가중치 값이 다르다.
물론 카테고리마다 연관성이 강한 뉴런에는 positive한 가중치를, 그렇지 않은 뉴런에는 negative한 가중치로 이어져 있을 것이다.
RBF Neuron Activation Function
]
RBF 의 각 뉴런은 입력과 training set에서 뽑은 prototype벡터간의 유사도를 측정한다고 앞서 언급하였다.
당연히 prototype과 유사한 input 벡터일수록 뉴런에서 1에 가까운 값을 출력할 것이다. 앞뒤가 바뀌게 설명했는데, 입력값과 prototype이 유사할 수록 해당 뉴런은 1에 가까운 값을 출력하는 것이다. 여러가지 유사도 함수가 존재하는데 가장 자주 사용되고 기본으로 사용되는 것이 가우시안 함수이다. 아래가 1차 입력에 대한 가우시안 함수이다.
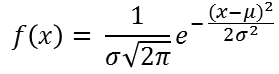
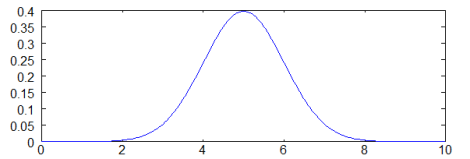
x가 입력이고 mu가 평균값이다. 시그마가 표준편차이다. 여기서 통계를 배운 사람들이 잘 아는 bell curve(정규분포)를 구할 수 있다. 아래 정규분포에서 중앙값이 평균값 5이며 sigma는 1이다.
RBFN의 전형적인 활성화 함수는 아래와 같다.
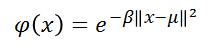
가우시안 분포에서 mu는 분포의 평균을 의미하며 여기에서는 위 bell curve(정규분포)의 중앙을 가리키는 prototype vector를 의미한다.
우리가 사용할 활성화 함수는 beta값이 1/(2*sigma^2)값이 된다.
위의 활성화 함수는 가우시안 함수에서 1/(sigma*sqrt(2*pi))가 제거되었는데 이 outer coefficent는 Gaussian함수의 높이를 조절하는 term이다. 이는 output 노드에 적용되는 가중치에 필요없는 부분이다. 위 outer coefficient를 제거하고, 학습과정에서 output노드는 정확한 계수(가중치)를 학습해갈 것이다.
beta값은 bell curve(정규분포)의 width를 조절한다.
[여기에서는 sigma를 신경쓰지 않고 beta로 간략화 시켜서 다루고 있다. beta에 따른 bell curve의 예시를 아래에서 확인할 수 있다.]
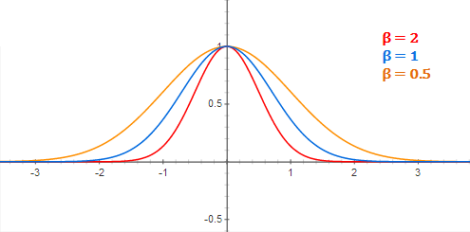
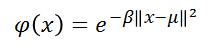
이 식에서 ||로 표기한것은 x와 mu사이의 유클라디안 거리를 계산하고 제곱함을 의미한다. 1차 가우시안에서 간략화된 식은 (x-mu)^2이다.
input이 prototype vector과 같을경우. || ||안의 값은 0이 되고 따라서 phi의 값은 최대인 1이 될것이다. 즉, 이를 통한 유클리디안 거리의 측정으로 우리가 input과 prototype간의 유사도 측정을 할 수 있음을 다시한번 상기하자.
prototype vector 으로부터 멀어질수록 그 응답은 지수적으로 감소한다. RBFN 구조를 다시한번 확인하면, 각 카테고리의 output node가 가중치를 거친 RBF neuron값의 합으로 이루어져 있으며, 따라서 모든 뉴런은 input에 대한 분류에 영향을 미침을 알 수 있다.
그러나, input vector와 prototype간의 거리가 멀 경우, 활성화 함수에 의해 지수적으로 그 값이 감소할 것인데, 결국 이는 해당 뉴런이 output의 결과에 거의 기여하는 바가 없음을 의미한다.(거의 반영되지 않는다는 뜻)
RBF Training.
prototype과 그 분포(분산)을 정하는 방법은 다양하다. 아래 논문에서는 RBFN의 학습을 위한 일반적인 방법을 제시하고 있다.
 10.1.1.109.312.pdf
10.1.1.109.312.pdf
Selecting the Prototypes.
What it really comes down to is a question of efficiency–more RBF neurons means more compute time, so it’s ideal if we can achieve good accuracy using as few RBF neurons as possible.
중요한 언급을 하고있기 때문에 그대로 끌어왔다. 여기서 언급하는 것은 RBF의 뉴런의 갯수가 늘어날 수록 연산시간이 길어질 것이며 따라서 우리는 최대한 적은 갯수의 뉴런을 사용하여 최대한의 정확성을 끌어내야 한다는 것이다.
블로그의 글쓴이는 이를 위해서 K-Means clustering을 통한 cluster center 결정 및 이를 prototype으로 사용할 것을 언급한다. 이는 RBF를 사용하는 다른 여러 이들도 사용하는 방법이다. 그러나 지금까지 찾아본 몇몇 알고리즘은 대부분이 많은 연산시간을 요구하였기 때문에 그 활용성에 의문이 갔었으나 해당 저자가 업로드한 알고리즘은 그 속도가 준수하였기 때문에 다음 글에서 이를 분석해보고자 한다. 이 글에서는 소개만 하도록 한다.
k-means 알고리즘을 사용하여, training example을 카테고리별로 중복없이 분류시켜야 한다.
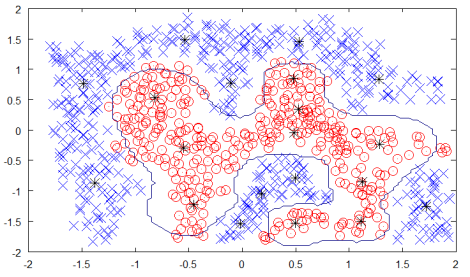
위 데이터시트를 보면 수많은 데이터들을 두 개의 클래스(카테고리)로 분류하였고 각 클래스마다 10개씩 총 20개의 뉴런에 대한 prototype을 선정하였다.(검은 별표가 prototype이다)
(위의 데이터시트는 기술적으로는 옳지 않다고 한다)
클래스로부터 얼마나 많은 클러스터를 선정할 수 있는지는 조건에 따르는데, 좋고 많은 결과를 얻기 위해서는 더 복잡한 조건의 설정이 필요하며 이에 따라 네트워크에서 더 많은 연선을 요구하게 된다.
Selecting Beta Values
k-means clustering을 통해 prototypes를 선정하였으면, 각 클러스터의 모든 pointer와 cluster center간의 거리에 대한 평균으로 sigma값을 구하고 이를 통해 beta값을 구하게 된다. 즉, 각 카테고리별로 해당 뉴런에 대응하는 클러스터 내의 중앙값 mu와 x값들간의 거리를 통해 아래와 같이 해당 뉴런의 sigma와 beta를 구하는 것이다.
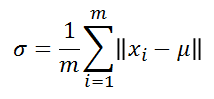
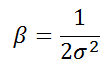
Output Weight
마지막으로 output에 대한 weight를 설정해야 한다. 이는 LMS(least mean square)의 gradient descent로 구하게 된다.
이와 관련해서는 다음 시간에 더 자세히 다루도록 한다.


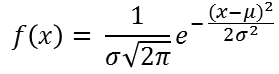

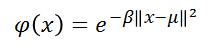

 10.1.1.109.312.pdf
10.1.1.109.312.pdf